Tema 1 - Lógica

Primer temita de FMI, basado en los apuntes de Nevado, Google y nuestro dios, salvador y maestro Gerardo Paredes Torres

Parte 1: Proposiciones/Op.Lógicos 🗣️🟰🧮

🗣️🗣️🗣️ Proposiciones

Una proposicion es una oración declarativa (en idioma natural) que puede tener 2 valores: Verdad(V) o Falso(F).

Nota

• RECUERDA Debe tener un valor y no los 2 al mismo tiempo, asi que es verdad ó falso.

Las proposiciones se asignan a una letra minusculas como r , s , p , q , etc y ejemplos de ellas son:

• r: ESPAÑA esta en Europa
• s: Alexis es GAAAAAY
• t: BOBR KURWA PIERDOLE
• p: Alexis le gusta Blanca y principalmente Cloe
• q: 69 / 3 = $\nexists$

Su valor de verdad se determina con V o F y a las proposiciones anteriores se les asigna uno

• t: BOBR KURWA PIERDOLE es V

🧮🧮🧮 Op.Lógicos

Un Operador Lógico es un elemento verbal/escrito que permite formar proposiciones (proposición compuesta) a partir de otras (proposición atómica).

Tipos de operadores lógicos

• Disyunción/O inclusivo —> Signo >>> "$\lor$" | Lectura >>> “O” $\Longrightarrow$ $\lor$ == O

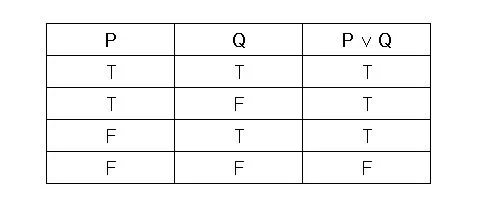
• Conjunción —> Signo >>> "$\land$" | Lectura >>> “Y” $\Longrightarrow$ $\land$ == Y

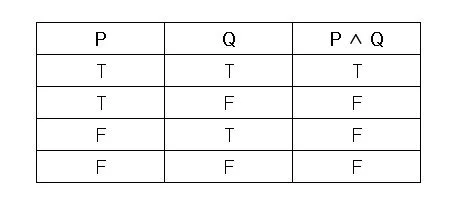
• Negación —> Signo >>> "$\neg$" | Lectura >>> “NO” $\Longrightarrow$ $\neg$ == NO

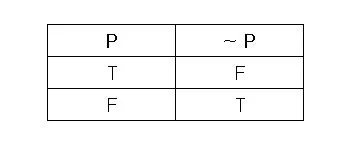
• O exclusivo —> Signo >>> "$\oplus$" | Lectura >>> “O… O…” (solo uno, no los 2) $\Longrightarrow$ $\oplus$ == O… O…

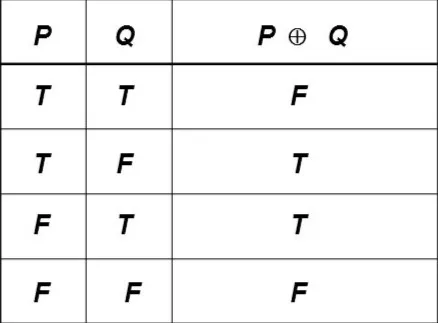
• Implicación —> Signo >>> "$\longrightarrow$" | Lectura >>> “Si… Entonces…” $\Longrightarrow$ $\longrightarrow$ == Si… Entonces…

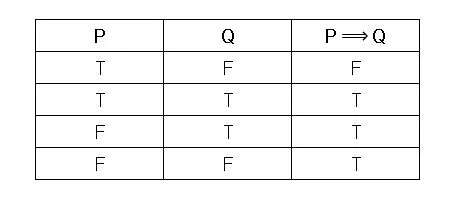
• Doble Implicación/Bicondicional —> Signo >>> "$\longleftrightarrow$" | Lectura >>> “…si, y solo si…” $\Longrightarrow$ $\longleftrightarrow$ == …si, y solo si…

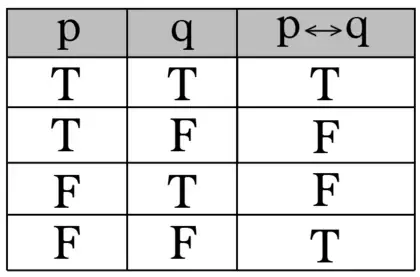
Tautología Always true ✅

Es una proposición que siempre es verdad, como puede ser: “A Carlos le gusta los porros —> V”.

Contradicción Always false ❌

Es una proposición que siempre es falsa, como puede ser: “Alexis no le gusta Cloe —> F”.

Contingencia Depende ❔❔❔

Es una proposición que depende de los valores de verdad de los elementos que forman la proposicion, asi que puede ser verdad o falso.

Parte 2: Equivalencias Lógicas 🥐🥐🥐

Relativas a OR , AND , NOT y IMPLICA

• Identidad (DNI)🪪

  P $\land$ V $\Longrightarrow$ P

  P $\lor$ F $\Longrightarrow$ P

• Dominación (Nyaa!)😺

  P $\lor$ V $\Longrightarrow$ V

  P $\land$ F $\Longrightarrow$ F

• Idempotentes (multiplicate por 1?)✖️

  P $\lor$ P $\Longrightarrow$ P

  P $\land$ P $\Longrightarrow$ P

• Doble Negación (NO CAMBIA NADA!!!)❌❌

  $\neg$ ( $\neg$ P) $\Longrightarrow$ P

• Conmutativas (Alexis x Cloe = Cloe x Alexis)💖

  P $\lor$ Q $\Longrightarrow$ Q $\lor$ P

  P $\land$ Q $\Longrightarrow$ Q $\land$ P

• Absorción (ÑAM ÑAM)🍔🍔🍔

  P $\lor$ (P $\land$ Q) $\Longrightarrow$ P

  P $\land$ (P $\lor$ Q) $\Longrightarrow$ P

• Asociativas (El parentesis es un cangrejo)🦀🦀🦀

  P $\lor$ (Q $\lor$ R) $\Longrightarrow$ (P $\lor$ Q) $\lor$ R

  P $\land$ (Q $\land$ R) $\Longrightarrow$ (P $\land$ Q) $\land$ R

• Distributivas (Como tu dealer de confianza)🌿🌿🌿

  P $\lor$ (Q $\land$ R) $\Longrightarrow$ (P $\lor$ Q) $\land$ (P $\lor$ R)

  P $\land$ (Q $\lor$ R) $\Longrightarrow$ (P $\land$ Q) $\lor$ (P $\land$ R)

• De Morgan (El tio preferido de POU CASTRO)🥔🥔🥔

  $\neg$ (P $\lor$ Q) $\Longrightarrow$ ( $\neg$ P $\land$ $\neg$ Q)

  $\neg$ (P $\land$ Q) $\Longrightarrow$ ( $\neg$ P $\lor$ $\neg$ Q)

• Equivalencia Fundamental de la Implicación (La unica importante…)💋💋💋 P $\longrightarrow$ Q $\Longleftrightarrow$ $\neg$ P $\lor$ Q

Parte 3: Predicados y Cuantificadores ❌❔❕

Predicados 🙊🙈🙉

Definición: Una sentencia P con variables “X1, X2, …Xn” se llama predicado P(X1,X2,…Xn) y se relaciona con un universo U (basicamente el conjunto de números que pertenece: R,N,Z,Q,etc).

Tambien se pueden realizar operaciones lógicas con los predicados:

• $\neg$P(X) $\Longrightarrow$ todo lo que no cumpla la sentencia P o su contrario.
• (P $\lor$ Q) (X) $\Longrightarrow$ todo lo que cumple la sentencia P o Q o las dos.
• (P $\land$ Q) (X) $\Longrightarrow$ todo lo que cumple la sentencia P y Q al mismo tiempo.

Cuantificadores 🧮🧾

• Cuantificadores Universales: $\forall$ $\Longrightarrow$ Para todo es el cuantificador que nos indica que P(X) se cumple en cada X de su dominio/universo, sus contraejemplo som que hay al menos 1 X que no cumple la proposición o ninguna X cumple la proposición.
• Cuantificadores Existencial: $\exists$ $\Longrightarrow$ Existe es el cuantificador que nos indica que P(X) se cumple al menos en una X de su dominio/universo, sus contraejemplo son que no hay ni una X que cumpla la proposicion o todas las X cumplen la proposición.
• Cuantificadores Existencial ÚNICO: $\exists!$ $\Longrightarrow$ Existe un único es el cuantificador que nos indica que P(X) se cumple solo y unicamente en una X de su dominio/universo, sus contraejemplos son que hay más de una X/todas las X cumplen la proposición o no hay una X que cumpla la proposición.

Nota

• $\exists!$ P(X) $\Longrightarrow$ $\exists$ P(X) $\land$ [ ( $\forall$ X1, $\forall$ X2, ( P(X1) $\land$ P(X2) ) $\longrightarrow$ X1=X2 ]

Negación Cuantificadores❌

$\neg$ ( $\forall$ P(X) ) $\Longrightarrow$ $\exists$ $\neg$ P(X)

$\neg$ ( $\exists$ P(X) ) $\Longrightarrow$ $\forall$ $\neg$ P(X)

$\neg$ ( $\exists!$ P(X) ) $\Longrightarrow$ $\forall$ $\neg$ P(X) $\lor$ [ ( $\exists$ X1, $\exists$ X2, X1 =/= X2, ( P(X1) $\land$ P(X2) ) ]

Cuantificadore aniñados/compuestos⚙️🛠️2️⃣

$\forall$ X, $\forall$ Y, P(X,Y) $\Longrightarrow$ para todo par de X e Y se cumple la proposición.

$\exists$ X, $\exists$ Y, P(X,Y) $\Longrightarrow$ al menos hay un par de X e Y donde se cumple la proposición.

$\forall$ X, $\exists$ Y, P(X,Y) $\Longrightarrow$ para todas las X, cada una tienen al menos una Y que cumple la proposición.

$\exists$ X, $\forall$ Y, P(X,Y) $\Longrightarrow$ existe al menos una X, que cumple la proposición para todas las diferentes Y del dominio/universo.

Parte 4: Razonamiento Deductivo 🧠💡🌻

Reglas de Inferencia 🤫🤫🤫

Basados en Tautologías y son equivalencias 100% equivalentes y intercambiables.

• Adición (Alexis = Alexis + Ser trapo)👠👠👠

  P $\Longrightarrow$ P $\lor$ Q

• Simplificación (Carrera Robar Manosear)🐒🐒🐒

  P $\land$ Q $\Longrightarrow$ P

• Conjunción (Bruno + Drogas = EL GUERRERO DRAGON)🐼🐉👲🏼

  (P) $\land$ (Q) $\Longrightarrow$ P $\land$ Q

• Modus Ponens (u cafe)☕☕☕

  P $\land$ ( P $\longrightarrow$ Q) $\Longrightarrow$ Q

• Modus Tollens (SYYYYYMPHOOOOOONYYYYY!!!)🐬🐬🐬🦄🦄🦄🌈🌈🌈

  $\neg$ Q $\land$ ( P $\longrightarrow$ Q ) $\Longrightarrow$ $\neg$ P

• Siloxismo Hipotético (Naya PHD Amor)💗💗💗

  ( P $\longrightarrow$ Q ) $\land$ ( Q $\longrightarrow$ R ) $\Longrightarrow$ P $\longrightarrow$ R

• Siloxismo Disyuntivo (bobby no te metas en el LOL…) 🐷🐷🐷

  ( ( P $\lor$ Q ) $\land$ ( $\neg$ P) ) $\Longrightarrow$ Q

• Ley de Resolución (Alexis x Miku es más probable que Alexis x Cloe D:)💘💘💘

  ( ( P $\lor$ Q ) $\land$ ( $\neg$ P $\lor$ R) ) $\Longrightarrow$ ( Q $\lor$ R )

Precaución

FALACIAS: razonamientos incorrectos basados en CONTINGENCIAS, no en tautologías, asi que cuidado de hacer cosas fuera de las equivalencias o inferencias

Parte 5: Metodos de demostración 👲🏼🐷👲🏼

Sistema Matemático ➕➖✖️➗

• Se suponen verdaderos los Axiomas
• Las Definiciones se utilizan para crear nuevos conceptos
• Se deducen Teoremas

Teoremas (Si como los de Nobita Nobi👆🏼🧐)

Una Sentencia que se puede verificar que es Verdad, suele venir como:

• P $\longrightarrow$ Q
• $\forall$ P(X)
• $\exists$ P(X)

Tipos de teoremas (Carlos deja el TCG y ponte a estudiar)♠️♥️♦️♣️♠️♥️♦️♣️

• Proposición: teorema pequeño
• Lema: teorema simple usado en otros teoremas
• Corolario: teorema comprobado por otros teoremas

Metodos demostración 🧐🧐🧐

Los metodos de demostración más usados y que nos tenemos que aprender son 3, realmente 4 si cuentas inducción, pero ese ya te lo sabes (verdad?????)

• Directa: pruebas el problema y le das la razon, osea, pruebas que es verdad
• Contra-Recíproco: pruebas la negación y dependiendo de su valor, el original es verdad o falso
• Reducción al Absurdo: llevas la proposicion a un punto absurdo, provando que obviamente lo que te dice la proposicion es verdad o falso
• Inducción: YA TE LO SABES HDP